“Boole Cebri” değişkenlerin değerinin doğru ve yanlış olabildiği bir cebir altkoludur. Doğru ve yanlış değerleri genelde sırasıyla 1 ve 0 olarak ifade edilir. Değişken değerlerinin sayı, işlemlerin ise toplama ve çarpma olduğu temel cebrin aksine Boole cebrinde ∧ işareti ile ifade edilen “ve”, ∨ işareti ile ifade edilen “veya”, ¬ ile ifade edilen “değil” işlemleri bulunur.
Boole cebri ismini George Boole’den alır ve bu ismin ilk kez 1913 yılında Sheffer tarafından önerildiği iddia edilmektedir.
Sayısal devrelerin analiz ve tasarımı boole cebrini temel alır. Bu sistemde yer alan “0” ve “1”, sırasıyla açık (ON) ve kapalı (OFF) devrelerle eş anlamlıdır. Sayısal bilgisayar devreleri uygulamasında, ikili değişkenler üzerinde tanımlanan sayısal operasyonları gösterir.
-> Wikipedia
Boole cebrinin temel kuralları aşağıdaki gibidir:
- a ∨ a = a a.a = a ( “∧” işlemi “.” ile de ifade edilebilir.)
- a ∨ b = b ∨ a a.b = b.a
- a.(b ∨ c) = a.b ∨ a.c a ∨ (b.c) = (a ∨ b).(a ∨ c)
- a ∨ (b ∨ c) = ((a ∨ b) ∨ c) a.(b.c) = (a.b).c
- (a’)’ = a (“¬” işlemi “ ‘ “ ile de ifade edilebilir.
- a’ ∨ b’ = (a.b)’ = a’.b’ = (a ∨ b)’
- a.b ∨ a.b’ = a (a ∨ b).(a ∨ b’) = a
- a ∨ a.b = a a.(a ∨ b) = a
- a ∨ 0 = a a ∨ 1 = 1 a ∨ a’ = 1
- a.0 = 0 a.1 = a a.a’ = 0
Boole cebri kuralları verilen boole fonksiyonunun daha sade bir hale getirilmesi için kullanılır.
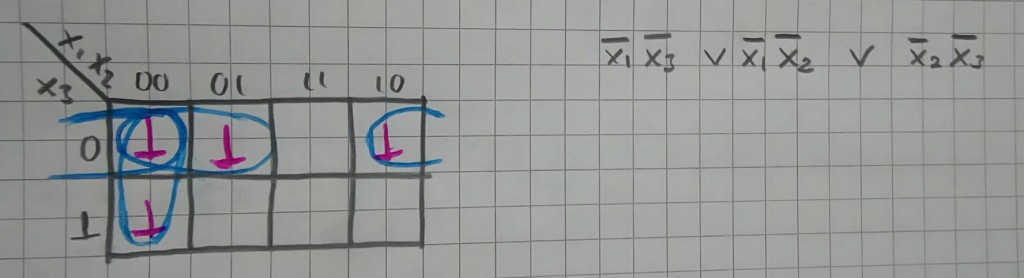
Boole fonksiyonlarının cebir kurallarına göre adım adım sadeleştirilmesindense karnough tablosuna yerleştirilip sadeleştirilmesi daha kısa bir yoldur.
Verilen 1’li durumlar karnough diyagramına yerleştirildikten sonra yan yana gelen 1 ler 2’nin katları şeklinde en fazla kaç 1 aynı grup içine alınabiliyorsa o şekilde gruplandırılır. Aynı grupta değişen bitler sonuç fonksiyonuna dahil edilmez.
http://bilgisayarkavramlari.sadievrenseker.com/2007/12/07/karnaugh-haritasi-karnaugh-map/

Bir yanıt yazın