Bu yazı dizisinin temeli Prof. Dr. Vasif Vagifoğlu Nabiyev’in Ayrık Matematik derslerine dayanmaktadır.
Ayrık matematik veya bazen kullanılan diğer adıyla sonlu matematik, matematiğin ayrık yapılarıyla ilgilenen süreklilik içermeyen konularını kapsayan matematik dalıdır.
Ayrık matematik son yıllarda bilgisayar mühendisliği uygulamalarındaki kullanımı nedeniyle ünlenmiştir. Bilgisayar biliminin temelidir.
-> Wikipedia
Bulanık Mantık -> 1961 yılında Lütfü Aliasker Zade’nin yayınladığı bir makale sonucu oluşmuş bir mantık yapısıdır. Bulanık mantığın temeli bulanık küme ve alt kümelere dayanır. Klasik yaklaşımda bir varlık kümenin ya elemanıdır ya değildir. Bulanık mantık klasik küme gösteriminin genişletilmesidir. Bulanık varlık kümesinde her bir varlığın üyelik derecesi vardır.
Klasik mantık = A veya A değil, kesin, 0 veya 1, ikili birimler.
Bulanık mantık = A veya A değil, kısmi, 0 ve 1 arasında sürekli, bulanık birimler.
Optimizasyon -> eldeki kısıtlı kaynakları en optimum biçimde kullanmaktır. Matematiksel olarak optimizasyon kısaca bir fonksiyonun minimize veya maksimize edilmesi olarak tanımlanabilir. “En iyi sonuçları içeren işlemler topluluğu.” “Maksimum kar minimum maliyet.”
n değişkenli bir fonksiyon için 2 üzeri n tane durum belirlenir.
n değişkenli bir fonksiyon için 2 üzeri 2 üzeri n tane fonksiyon tanımlanır.
⇒ Bir kağıdı önce 3 parçaya bölüp sonra o parçalardan birini alıp tekrar üç parçaya böldüğümüzü varsayalım. Bölme işlemi 5 kez tekrarlandığında elimizde kaç parça kağıt olur?
Genellikle problemlerin araştırılmasında nesneler ve bu nesnelerin kontrolü olmak üzere iki bileşen ele alınmaktadır. Uygulamalarda kontroller nesne modelleri üzerinde gerçekleştirilmektedir. Modeller sürekli ve ayrık olmak üzere iki alt sınıfa bölünür. Genellikle nesnenin yapı özelliği ele alındığında ayrık stille mantıksal fonksiyonlar yardımıyla ifade edilir. Sistemin davranışı zaman fonksiyonu şeklinde verilir.
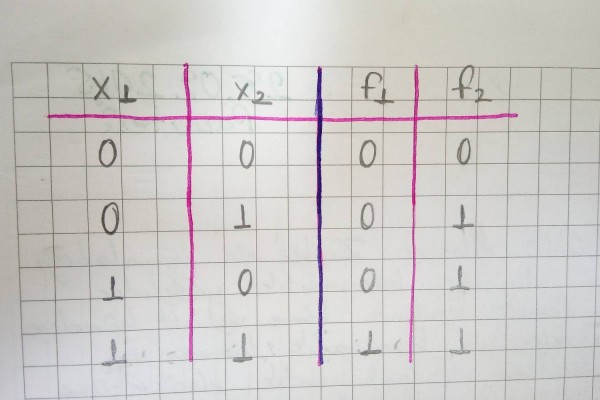
f (x1,x2,…. ,xn) fonksiyonunun ve argümanlarının değerleri yalnız 1 veya 0 ise bu fonksiyone ve benzer fonksiyonlara Boole Fonksiyonları (BF) denir. Bir Boole fonksiyonu analitik veya tablo biçiminde verilebilir. Fonksiyonun aldığı değerler doğruluk tablosu şeklinde ifade edilir.
Veitch tablosunda durumlar doğruluk tablosundaki normal sıralamalarına göre yerleştirilirler. Karnough tablosunda ise 1 bitlik değişime göre yerleştirilirler.




Bir yanıt yazın