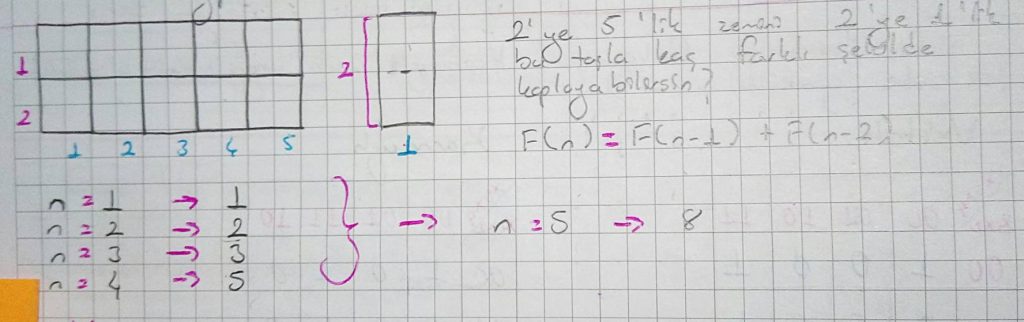
Şekildeki örnekte cevap Fibonacci Sayılar olarak karşımıza çıkar. Bu bir alanın belirli bir parça ile olan tüm kapsama şekillerini verir. Konu olarak ele aldığımız ” Kapsama Problemi ” de buna benzemektedir.
Eğer tabloda [i,j] = 1 ise i. satır j. sütunu kapsıyor denilir. Aşağıdaki iki şartı sağlayan durumlara kapsama denir;
- Herhangi sütun bu kümenin (kapsamanın) satırı ile kapsanmış olur.
- Bu kümenin elemanları fazlalık içermemektedir.
Kapsama “π” ile gösterilir.
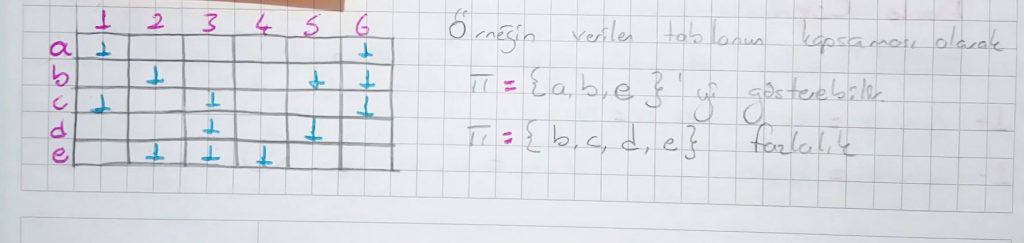
Kapsama problemine örnek olarak bir şirketin işe alımını düşünelim. a, b, c, d, e işe başvuran elemanlar; 1, 2, 3, 4, 5, 6 ise şirketin çalışma günleri olsun. a satırındaki 1 bulunan sütunlar a elemanının çalışabileceği günler olur. Buna göre şirket tüm günleri en az eleman ile doldurmalıdır. Bu tablomuzun minimum kapsaması olur. Yani en az eleman ile tüm günleri kapsama gibi düşünebiliriz. Diğer kapsamalar ise fazlalıktır.
Kapsama problemlerinde genellikle iki alt problem ele alınmaktadır;
- Minimum kapsamanın bulunması
- Tüm kapsamaların bulunması
Tüm kapsamaların bulunması için Patrick yönteminden faydalanılır. Patrick yöntemine göre her bir sütun değeri toplamlar şeklinde ifade edilerek bu sütunların çarpım sonucu aranmaktadır. Yukarıdaki tablonun tüm kapsamaları şu şekildedir;
π = (a v c).(b v e).(c v d v e).(a v e).(b v d).(a v b v c) -> tüm sütunları toplamların çarpımı şeklinde yazdık, bu fonksiyonu Boole fonksiyonlarına göre sadeleştiriyoruz.
= (a v ce).(b v de).(e v ad v ae v bd v be)
= abc v abd v abe v ade v bce v cde -> Tüm kapsamalar
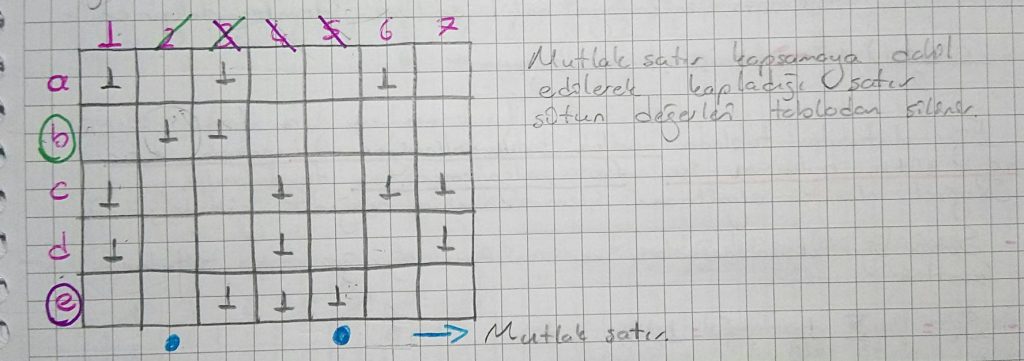
Minimum kapsamanın bulunmasında ilk önce tablonun sıkıştırılması gerçekleştirilir. Bunun için ilk olarak tabloda mutlak satır (eğer bir sütunda sadece tek bir tane “1” var ise bu sütunun kapsanması için sütundaki “1” olan satır mutlak satırdır.) olup olmadığı araştırılır. Mutlak satır olarak kapsamaya dahil edilmek zorundaki satırlar tablodan kapsadıkları diğer sütunlar ile birlikte silinir ve kapsamaya dahil edilir.
Geriye kalan daraltılmış tabloda ise kapsamayı tamamlayacak satır bulunup kapsamaya eklenir.
Şekilde c satırı seçildiğinde kapsanmamış sütun kalmadığından o kapsamaya dahil edilir.
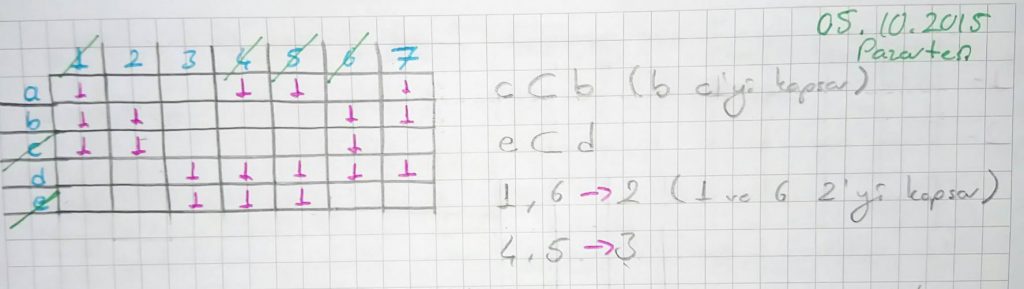
Eğer tabloda mutlak satır yok ise minimum kapsamanın bulunmasında kapsayan satır ve kapsanan sütun kavramlarından faydalanılır. Eğer B С A ise A satırı kapsayandır.
Sütunlar için |M| = |N|+1 ve N С M ise M kapsanan sütundur. (Sütunda daha çok eleman olması o sütunu kapsayabilmek için daha çok elemanın olduğu anlamına gelir. Yani kapsayan satır daha çok elemanlı iken kapsayan sütun daha az elemanlı olandır.) Kapsanan satır ve sütunlar tablodan silinir.
Kapsanan satır ve sütunlar tablodan silindikten sonra aşağıdaki değerler elde edilir;
Genel olarak kapsama probleminin çözümünde mutlak satır bulunmadığında kapsanan satır ve sütunlar ardışık şekilde elenmekte, mutlak satır oluştuğunda bu satır kapsamaya dahil edilmektedir. Kapsama tamamlanana kadar işlemler ardışık olarak tekrar edilir.
[ n . ( n-1) ] / 2 -> karşılaştırma sayısı


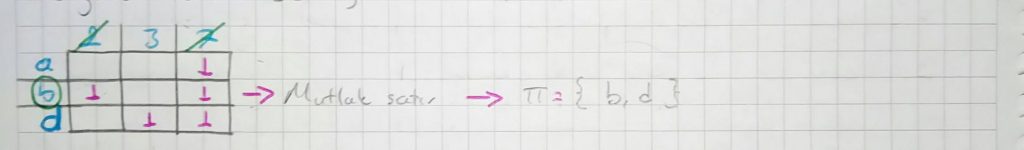
Bir yanıt yazın