İlk yazımızda sadece 0 ve 1 değerleri alabilen fonksiyonlara Boole Fonksiyonları denildiğinden bahsetmiştik. Boole fonksiyonları çok sayıda bit ile ifade edilebilir, bu yazıda Boole fonksiyonlarının minimize edilmesi yani daha az değişken ile ifade edilmesi için uygulanan adımları işleyeceğiz.
Boole fonksiyonlarının değişken sayısının azaltılması için çeşitli yöntemler kullanılmaktadır. Bunlara örnek olarak Karnough tablosunu, Mc Cluskey yöntemini gösterebiliriz. Bundan önce fonksiyonların minimizasyonunu anlamak için onların hypercube (hiperküp) tasviri önemlidir.
Değişken sayısına göre şekil karmaşıklığı artmaktadır.
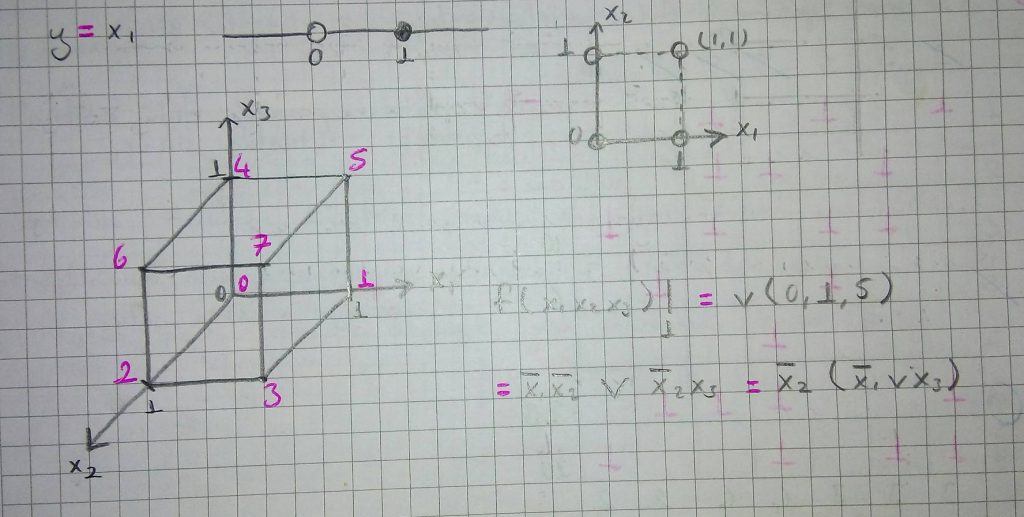
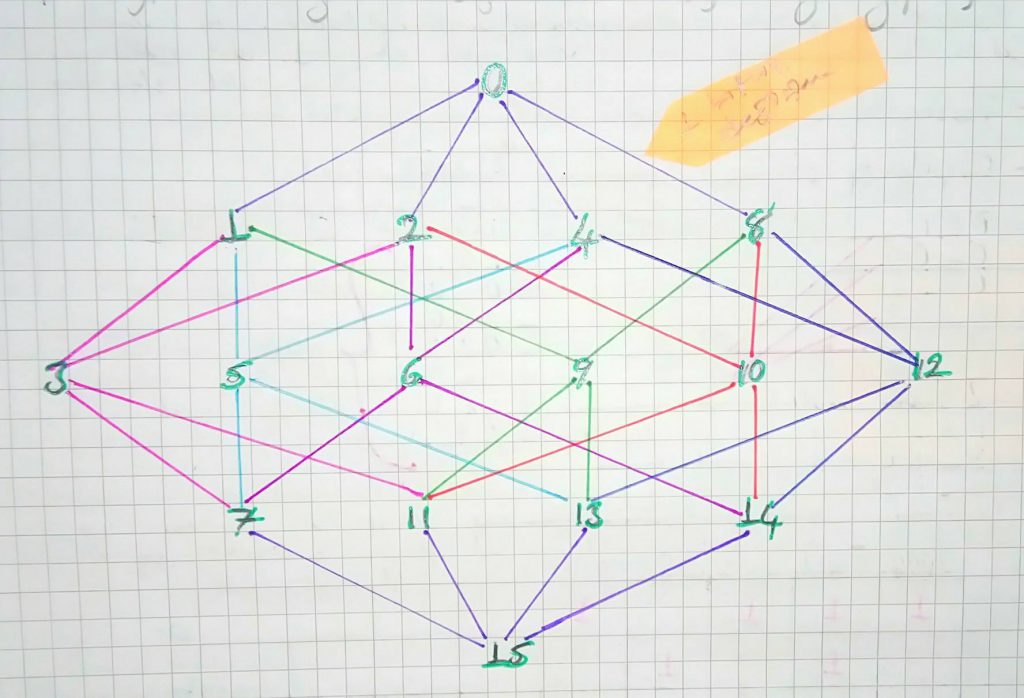
4 değişkenli fonksiyonlar için hypercube tasviri aşağıdaki şekilde yapılır;
Hypercubede katmanlar 1 bitlik değişime göre oluşturulur. Örneğin yukarıdaki çizimde 0 birinci katmandır ve ikinci katman olan 1, 2, 4 ve 8’ e 0’dan (0000) sadece 1 bit değişim ile geçilir.
y = ab’c’ v a’d
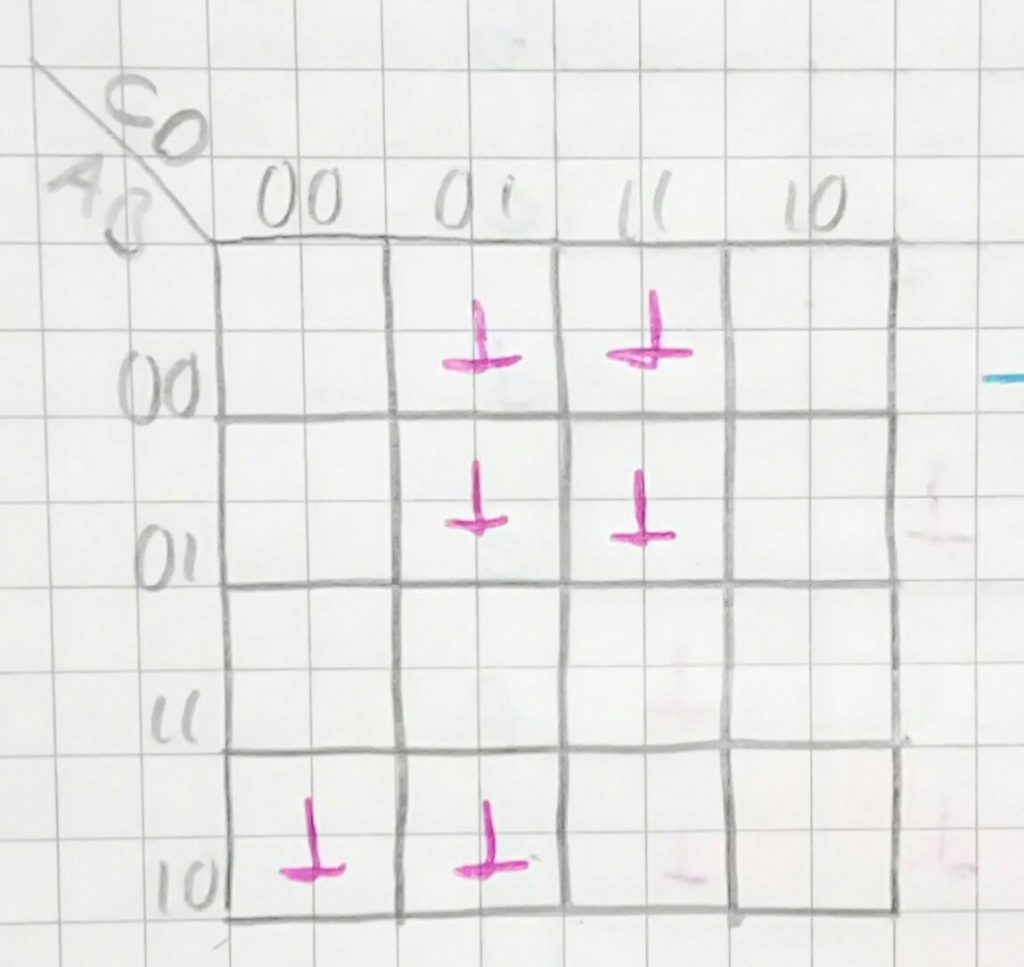
4 bitlik Boole fonksiyonlarının minimizasyonu için en uygun yöntem Karnough tablosuna yerleştirip sadeleştirmektir. Ama Değişken sayısı arttığında bu tabloyu oluşturmak çok fazla zaman alacaktır.
Diğer yöntem için aşağıdaki fonksiyonun minimizasyonunu ele alalım;
Fonksiyon 9 durum ile ifade edilmiş, her durum 4 bit olduğundan bu fonksiyonun karmaşıklığı 36’dır ve 36 karmaşıklı fonksiyonda işlem yapmak zordur bu nedenle minimize edilmeli. İlk olarak verilen 1’li durumlar hypercubedeki 1 bitlik değişime göre katmanlar halinde sıralanır.
0000  0001 0100 0011 0101 1100 1011 1110 1111
0001 0100 0011 0101 1100 1011 1110 1111
Boole fonksiyonlarının minimizasyonu aralıklar yardımı ile gerçekleştirilir. Bu şekilde verilen fonksiyonlar için işlem 2 aşamalıdır.
- Verilen durumları ifade eden maksimum aralıkların belirlenmesi.
- Implicant tablosu oluşturularak fazlalıkların çıkarılması.
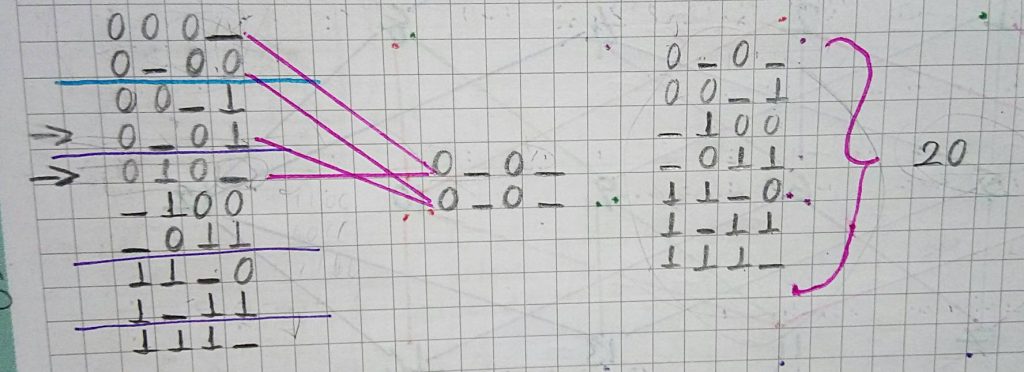
Katmanlar yazıldıktan sonra komşu katmanlar yukarıdan aşağıya doğru (1. Katmanla 2. Katman , 2. İle 3. Katman, 3. İle 4. Katman , 4. Katman ile 5. Katman şeklinde) karşılaştırılarak 1 bitlik değişim olan noktalara “_ ” yazılır. Daha sonra aynı ifade ile temsil edebilecek olanlar tek bir ifade ile gösterilir, bu maksimum aralıkların bulunması işlemidir.
Aralıkların bulunması ile karmaşıklık 36 dan 20 ye (20 bit) inmiş oldu. İkinci aşamada Implicant tablosunu oluşturuyoruz. Tablonun sol tarafına satır başlarına aralıklar, üst tarafına sütun başlarına ise fonksiyonda verilen 1’li durumlar yerleştirilir. Satırdaki aralık değeri ile ifade edilebilecek (yani “_ “ olan yerlere 0 veya 1 yazılarak oluşturulabilecek durumlar (sütunlar)) durumlar 1 değeri alır.
Tabloyu doldurduktan sonra tüm kapsamalarını bulmamız gerekiyor. Tüm kapsamaları bulmak için Patrick yöntemini kullandığımızdan daha önce bahsetmiştik. İşlemleri kolaylaştırması için satırları a, b, c gibi isimlendiriyoruz. Patrick yöntemi ile tüm kapsamaları hesapladıktan sonra bizim için uygun olan (en az bit sayısına sahip olan) minimum kapsamayı seçiyoruz.
Minimum kapsama (seçtiğimiz abef kapsaması) ile fonksiyon 11 bit ile ifade edilebildi. Yani fonksiyonun karmaşıklığı 36’dan 11’e indirgenmiş oldu.
Umarım anlaşılır olmuştur =)

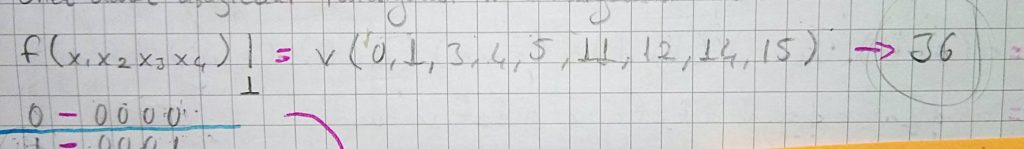


Bir yanıt yazın