Ayrık Matematik Kapsama Problemi konusunda mutlak satır olması ve Kapsanan satır, sütun olması durumlarında kapsamanın yazılmasını anlatmıştık. Bu yazıda ise Rota Algoritması ‘nı anlatmayı deneyeceğim.
Eğer oluşturulan tabloda mutlak satır yoksa, kapsanan satır ve sütun bilinmiyorsa “ Rota Algoritması ” ndan yararlanılır. Sezgisel olan bu algoritmanın adımları aşağıdaki gibidir;
- Sütun ağırlıkları hesaplanır ve minimum ağırlığa sahip satırlar işaretlenir. (sütun ağırlığı o sütunda bulunan tüm 1’lerin toplamı demektir.)
- 2. Sk = m ∑ 1/αi , i = 1, 2,….t
İşaretlenmiş satırların (sütun ağırlığı en az olan sütunlarda 1 değeri olan satırlardır.) ağırlıkları yukarıdaki formül ile hesaplanır. Burada Sk -> k. Satırın ağırlığı, m -> satır sayısı, t -> satırdaki “1” değerinin bulunduğu sütundaki toplam 1’lerin sayısı, αi -> satır 1’leri demektir. - Minimum ağırlığa sahip olan satır seçilerek tablodan silinir.
- Mutlak satırlar kapsamaya dahil edilir ve tablo sıfırlanana kadar 1-3 adımları tekrarlanır.
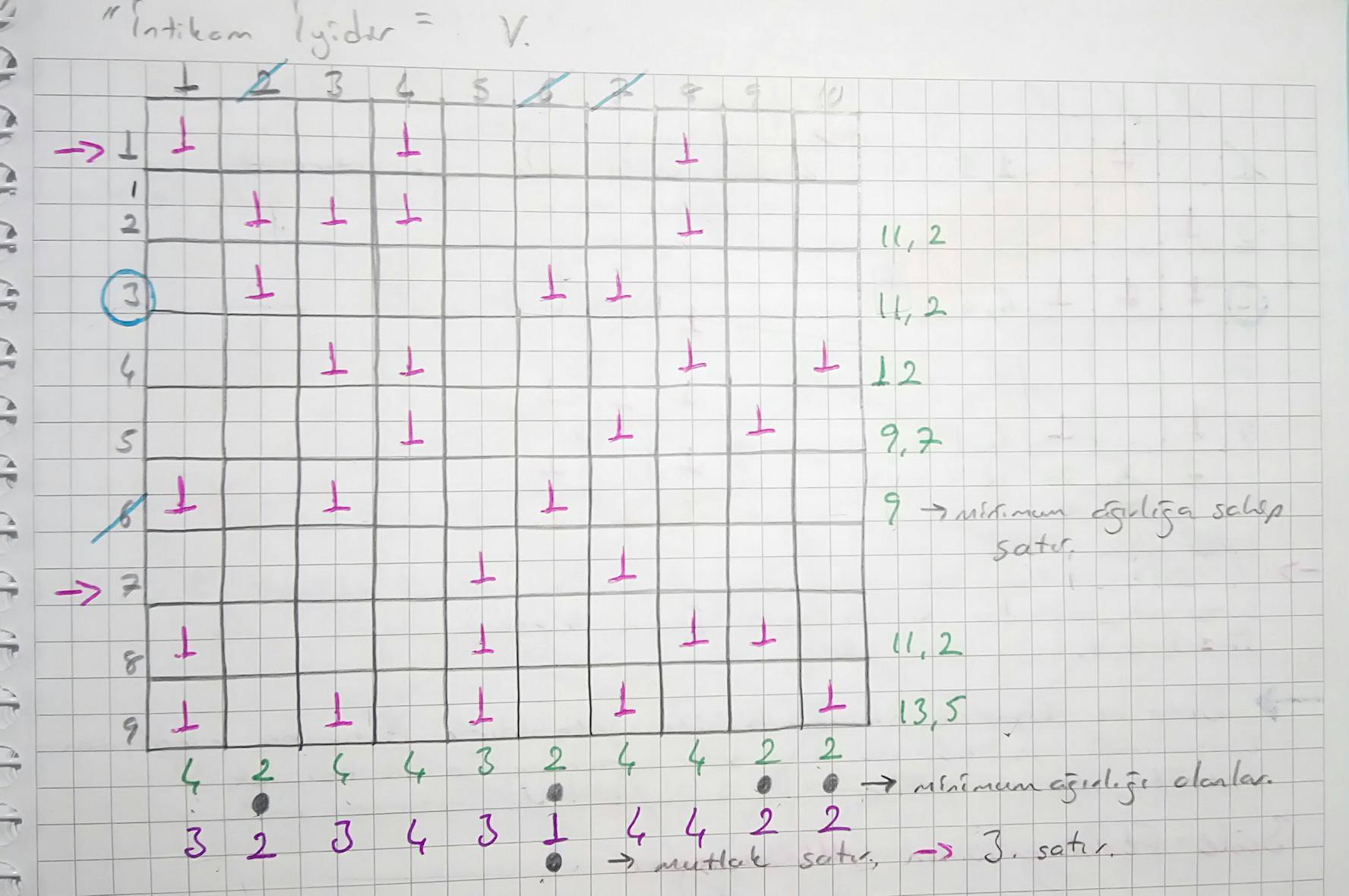
Öncelikle sütun ağırlığını hesaplıyoruz, örneğin birinci sütun için 1. satırda, 6. satırda 8. ve 9. satırlarda 1 vardır yani toplamda 4 tane bunu yeşil renkle tablonun altına yazdık. Tüm satırlar için bu işlemi yaptıktan sonra minimum ağırlıklı sütunları işaretliyoruz. Bu tablo için minimum ağırlıklı olan sütunlar altında nokta bulunan 2 ağırlıklı 2. 6. 9. ve 10. sütunlardır.
Bu sütunlarda 1’i bulunan satırların verilen formül ile ağırlıkları hesaplayıp tablonun sağ tarafına yazdık, örneğin 2. sütun için 2. ve 3. satırlardır. Hepsi için satır ağırlıklarını bulduktan sonra minimum ağırlıklı -9- olan 6. satırı tablodan siliyoruz. 6. satırı tablodan çıkardıktan sonra oluşan mutlak satırları kapsamaya dahil edip o satırları ve kapsadıkları sütunları da tablodan çıkarıyoruz. Tabloda kapsanmayan satır ve sütun kalmayana kadar işlemleri tekrar ediyoruz. (tabloda ilk aşamada 5. satır ağırlığı 9 çıkmaktadır, 6. ve 3. satır çıkarıldıktan sonra ikinci aşamada 9.7 çıkmaktadır, isterseniz ilk aşamada 6. satır yerine 5. satırı da silebilirsiniz.)
- satır mutlak satır olduğundan kapsamaya dahil edilerek 3. , 4. ve 10. sütunlar tablodan silinir ve minimum kapsama olarak π = { 3, 8, 4 } elde edilir.
-> Satır ve sütun ağırlıklarının birbirine eşit olduğu durumlarda algoritmanın devam ettirilebilmesi için rastgele bir satır kapsamaya dahil edilerek işlemlere devam edilir.

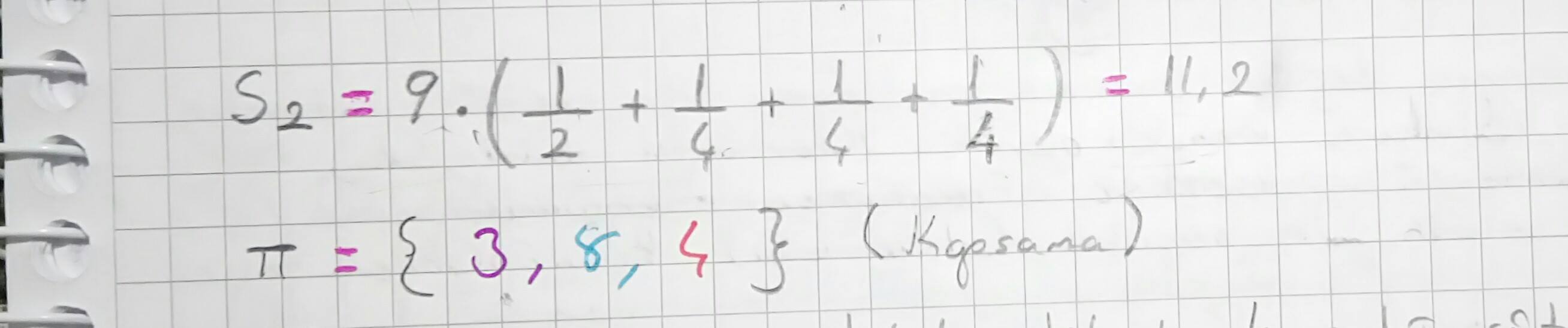


Bir yanıt yazın