Sezgisel Arama Algoritmaları, D* Lite

Sezgisel arama algoritmaları birçok kullanım alanı olan çok geniş ve detaylı bir konu. Türkçe olarak çok fazla içerik bulunmayan bu konu ile ilgili yol planlama alanında kullanılan ufak bir kısmını ve ağırlıklı olarak D* Lite algoritmasını temel bir fikir vermesi adına sizler ile paylaşmak istiyorum.

A* Algoritması

A* Algoritması başlangıç düğümünden bitiş düğümüne olan en az maliyetli yolu bulmada kullanılır [33]. A* ilk olarak 1968 yılında kullanılmıştır [34]. GBFS’nin olduğu gibi sezgisel arama algoritmasıdır. A yıldız(A*) Algoritmasında farklı olarak bilinen bir gerçek değer vardır. Bu değer sezgisel tahmin değerine eklenerek sezgisel fonksiyon hesaplanır [35].

En kısa yol hesaplanırken; toplam maliyet işlevi f(x), uzaklık işlevi g(x) ile buluşsal (heuristic) işlev h(x) toplanarak elde edilir [36].

f(x) = g(x)+ h(x)

Yol maliyet işlevi g(x), başlangıç düğümünden üzerinde bulunulan düğüm arasındaki yol uzunluğu ile hesaplanır [36]. h(x) işlevi buluşsal işlev olarak adlandırılır, bu işlev ise üzerinde bulunulan düğüm ile bitiş düğümüne bakılarak bulunur. h(x) bitiş düğümüne kadar olan düz bir çizgiyi temsil edebilir, fiziksel olarak ise iki nokta arasındaki mümkün olan en kısa mesafedir [37].

Dijkstra Arama Algoritması

Algoritma işleyişini bir örnek üzerinden inceleyelim.

1.      O = {S}

2.      O = {1, 2, 4, 5}; C = {S} (1,2,4,5‘in geri dönüş düğümleri S)

3.      O = {1, 4, 5}; C = {S, 2} (C içerisine düğüm eklenmiyor)

4.      O = {1, 5, 3}; C = {S, 2, 4} (1, 2, 4’ün geri dönüş düğümleri S; 5’in geri dönüş düğümü 4)

5.      O = {5, 3}; C = {S, 2, 4, 1}

6.      O = {3, G}; C = {S, 2, 4 1} (Hedef düğüme S -> 4 -> 5 -> G şeklindeki yol izlenerek ulaşılır.) [38].

Burada S başlangıç düğümü, G hedef düğümü temsil etmektedir. O (Open) ise açılan düğümleri, C (Close) kapanan düğümleri listeler.

Bu algoritmada çözümün uzunluğuna göre arama alanı üssel olarak büyümektedir.

D* Algoritması

D* Algoritması, 1994 yılında Anthony Stentz [39] tarafından tanıtılmıştır. D* adı “Dinamik A” teriminden gelmektedir. Çünkü D Algoritması çalışırken ark maliyetlerinin değişebilmesi dışında A* gibi davranır.

D* (Dinamik A) Algoritması, kısmen bilinen, bilinmeyen veya değiştirilen alanlarda yol planlaması yapabilir. D ve varyantları mobil robot ve özerk araç navigasyonu için yaygın olarak kullanılmaktadır.

D* Algoritmasının yürütülmesi, ilk planlama ve yeniden planlama aşamalarına ayrılabilir. Robotun başlangıç konumunda durması durumunda ilk planlama yapılır ve robotun hareketi sırasında değişen engellerin olduğu düğümleri tespit etmesi durumunda yeniden planlama yapılır.

A* gibi, D*, “OPEN list” (var olan listeyi temsilen “AÇIK liste”) olarak bilinen düğümlerin bir listesini tutar. Düğümler birkaç durumdan birine sahip olarak işaretlenmiştir [40].

• YENİ (NEW), düğüm AÇIK(OPEN) listesinde hiç bulunmuyor demektir.
• AÇIK(OPEN), düğümün şu anda AÇIK(OPEN) listesinde olduğu anlamına geliyor.
• KAPALI(CLOSE), düğüm artık AÇIK(OPEN) listede değil.
• Maliyetinin AÇIK(OPEN) listesindeki en son fiyattan daha yüksek olduğunu belirten düğüm işareti: ARTIŞ(RAISE)
• DÜŞÜŞ(LOWER), düğümün maliyetinin AÇIK(OPEN) listesindeki en son fiyattan düşük olduğunu gösterir [40].

D* Algoritması optimaldir. Geniş ve karmaşık alanlarda daha verimlidir. Geri dönük hesaplama maliyetinden kaçınır [38].

Odaklanmış (Focused) D* Algoritması

Odaklanmış D* Algoritması sezgisel g (X, R) fonksiyonu ile robotun R konumundan X konumuna kadar tahmini bir yol maliyeti olduğunu belirtir. Bu algoritma genellikle robotun; tutarsızlıkları bulduktan bir süre sonra hareket ettiğini varsayar [38].

D* Lite Algoritması

Özerk araç navigasyon problemini çözmek için D* Lite Algoritması tasarlanmıştır. Koenig’in, artımlı aramayı içeren A* araştırmasının bir türevi olan, Yaşam Boyu Planlama A* (Lifelong Planning A*) uyarlamasıdır. Artımlı arama yöntemleri, her arama görevini sıfırdan çözerek mümkün olandan çok daha hızlı bir şekilde benzer sorunlara çözümler bulmak için önceki aramalardan gelen bilgileri yeniden kullanır.

D* Lite Yöntemi, D* yöntemi ile aynı şekilde davranır, ancak algoritma olarak D‘dan farklıdır. Bu yöntem basittir, kesin olarak analiz edilebilir, genişletilebilir ve D kadar verimlidir.

D* Lite A* ‘a dayanır. Bekleyen düğümleri öncelik sırasına göre saklar. Düğümler nesnel fonksiyon değerlerine göre artan sırada saklanır. Haritada değişiklikler meydana geldiğinde çözüm yollarını aşamalı olarak arar. Hızlı yeniden planlama yapar. D* ile benzer işlevselliktedir ama daha basit bir algoritmaya sahiptir [38].

D*Lite Algoritması düğüm başına iki maliyet tahmini tutar;

g -> nesnel fonksiyon değeri. Biz ne biliyorsak ona dayanır. (adım sayısı gibi)

rhs -> nesnel fonksiyon değerinin bir adımlık görünüş tahmini.

Tutarlılık tanımı ise şu şekilde yapılır;

Tutarlı -> g = rhs

Tutarsız -> g ≠ rhs

Tutarsız düğümler işlenmek için öncelik kuyruğuna (open list) alınır. Geri dönüş düğümü bilgisi tutulmaz [38].

Grafikte a’dan b’ye yönlendirilmiş bir kenar var ise b’nin a’nın ardılı olduğu ve a’nın b’nin öncülü olduğu söylenir [38].

     Bir düğümün rhs değeri; grafikteki haleflerin g değerlerine ve kenarların bu haleflere geçiş maliyetlerine dayanarak hesaplanır. (g değeri “0” olan hedef noktasından başlanarak.) [38]

Açık listedeki bir düğümün anahtarı/önceliği g’lerin minimumudur ve rhs değeri ile sezgisel fonksiyon değeri olan h’ın toplamıdır [38].

Daha iyi anlaşılması için aşağıdaki örneğin adımları ile incelenmesi faydalı olacaktır.

     Şekilde yol maliyetlerinin hesabı aşağıdaki şekilde yapılacaktır.

     Örnekte sezgisel fonksiyon kullanılmamıştır ( h = 0). Başlangıçta hedefin rhs değeri 0, diğer tüm düğümlerin rhs ve g değerleri ∞ olarak ayarlanır.

     Asgari öğe açık listeye alınır (hedef). Aşırı tutarlıdır. (g > rhs) g = rhs olarak güncellenir.

     Küçük oklar hangi düğümün rhs değerini hesaplamak için kullanıldığını gösterir. Örneğin (0,1)’in rhs değeri (0,0)’ın g değeri ve (0,1) ile (0,0) arasındaki geçiş maliyeti kullanılarak hesaplanır.

1 = 0 + 1

     Açık listeden minimum öğe açılır, (0,1) aşırı tutarlıdır (g > rhs) bu yüzden g = rhs yapılarak güncellenir.

     Açılan düğüm (0,1) genişletilir. Seleflerin rhs değerleri hesaplanır ve tutarsız hale gelenler açık listeye eklenir.

     Bazı öncüllerin örneğin (0,0) ve (1,1) ‘in rhs değerleri değişmemektedir. Dolayısıyla tutarsız hale gelmezler ve bu aşamada tekrar açık listeye eklenmezler.

Açık listeden tekrar minimum değere sahip olan öğe açılır. (1,0) aşırı tutarlıdır (g > rhs) bu yüzden    g = rhs olarak güncellenir.

     Açılan düğümün yani (1,0)’ın genişletilmesi gerekir ama bu noktada seleflerin rhs değerleri bu düğümlerde engel olduğu için azaltılamaz. Bu yüzden bu düğümler açık listeye alınamaz. Düğüm genişletilemez. Adımlara devam edilerek açık listeden minimum değere sahip olan öğe açılır. (0,2)        g > rhs olduğu için aşırı tutarlıdır. g = rhs şeklinde güncellenerek açılır ve açılan düğümde genişletme işlemi yapılır.

     Açık listeden minimum değere sahip olan (1,2) düğümü seçilip açılır. g > rhs -> g = rhs

     Açık listeden tekrar minimum değere sahip olan öğe açılır. (0,3) için g değeri güncellenir. Bu düğümde genişletilecek yani açık listeye eklenecek yeni düğüm yoktur. Açık listeden minimum değerdeki sonraki düğüm (1,3) açılır ve g değeri g = rhs şeklinde güncellenir. Bu düğümünde genişletilecek komşusu olmadığı için listeden (2,2) düğümü açılır. g değeri güncellenip düğüm genişletilir.

     Açık listeden minimum değerdeki (2,3) düğümü açılır. Bu düğümden genişletilecek yeni düğüm olmadığı için sıradaki düğüm (3,2) açılır. Bu düğümden genişletme işlemi yapılır.

     Başlangıç düğümü açık listeye eklendi ama arama bu noktada tamamlanmıyor. Açık listeden minimum değerdeki eleman (3,3) seçilerek açılır. Bu düğümden sonra ise (3,1) düğümü açılır ve genişletilir. Sonra ise minimum değerdeki (4,2) düğümü açılır. Açık listede olmayan komşu düğümü kalmadığı için genişletilemez. Bu noktada başlangıç düğümü tutarlıdır ve açık listedeki üst anahtar başlangıç düğümününkinden daha az değildir. Bu yüzden en uygun yol oluşmuş kabul edilir ve döngüden çıkılır. Açık listede hala düğümler olduğu unutulmamalıdır. Daha büyük haritalarda hiç bakılmamış düğümler bile kalabilir. En uygun yol bulununca iterasyonlar biter.

Yol oluşturulurken başlangıç durumundan g değerlerinin derecesi izlenir.

     Robot yolu takip edip (3,2) ‘den (2,2) ye giderken bir engel olduğunu keşfettiğini varsayalım. Bu aşamada yeniden planlama gerekir. Etkilenen tüm kenarlar için yeniden hesaplama yapılır. Bu da (2,2) ‘nin komşusu olan 8 düğüm için 16 kenar demektir (çift yönlü oldukları için). İlk önce (2,2) ‘den komşuları yönüne olan kenarlar hesaplanır. (2,2) ‘nin rhs değeri “∞” olur.  Açık listeye alınır ve g ≠ rhs olduğu için tutarsızdır. Daha sonra komşularından (2,2) ‘ye gelen kenarların maliyetleri tekrar hesaplanır. (2,2) ‘nin rhs değeri ∞ olduğu için bu düğüm kullanılarak açılan tüm düğümlerin maliyeti değişir.

(2,2)’nin komşularından biri (3,3)’tür, bu düğümün rhs değeri 4,8’dir. Bu değer (2,2) ‘den değil artık (2,3) ’ten gelmektedir, hala tutarlı durumda olduğu için açık listeye alınmaz.

(2,2)’ nin diğer bir komşusu (3,2) ‘dir. (2,2) ‘nin geçiş maliyetinin artması nedeniyle (3,2)’ nin geçiş maliyeti (2,3) ’ün g değerine göre hesaplanır, yeni g değeri 5,2 olur. g ≠ rhs olduğundan tutarsızdır, bu sebeple açık listeye alınır.

     (2,2) ‘nin bir diğer komşusu (3,1) ‘dir. (3,1) ‘in rhs değeri (3,2) ‘nin g değerine göre 5,4 olarak hesaplanır. g ≠ rhs olduğundan tutarsızdır ve açık listeye eklenir. Diğer komşuları kendisinden açılmadığı için tutarsızlığa neden olmaz. Şimdi en uygun yol yeniden hesaplanana kadar algoritma tekar çalıştırılır. Robotun şuanki  konumuna karşılık gelen düğüm tutarsız ve açık listedeki minimum anahtardan büyük değere sahip. Bu nedenle henüz en uygun yolun bulunmadığı kabul edilir.

     Açık listeden minimum değere sahip eleman (2,2) seçilir. Düşük tutarlıdır g < rhs, g = ∞ olur. Açılan düğüm genişletilir ve tutarsız hale gelen düğümler açık listeye eklenir. Bu düğüm için açık listeye alınacak düğüm yoktur.

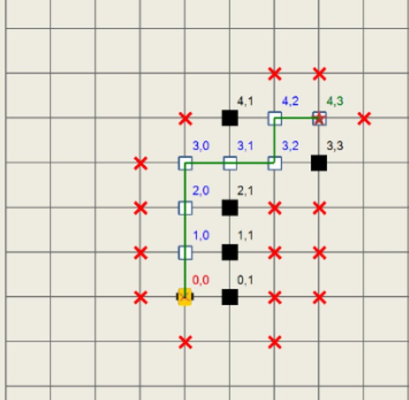
İterasyonlar takip edilerek açık listeden minimum değere sahip eleman (3,2) seçilir.   g < rhs olduğundan düşük tutarlıdır. g = ∞ olarak güncellenir ve düğüm genişletilir. Değerler güncellenir, (4,2) tutarsız hale gelir. (3,1) güncellenir, hala tutarsızdır. (4,1) ‘in rhs değeri değişmez ancak şuan (3,1) ‘in g değerine göre hesaplanmaktadır.

     (3,2) açıldığında hala tutarsız olduğundan açık listeye tekrar eklenir.

Açık listeden minimum değere sahip olan (3,1) düğümü seçilir. g < rhs olduğundan düşük tutarlıdır, g = ∞ olur. Düğüm genişletilir. Değerler güncellenir. (4,1) güncellenir ama hala tutarsız olduğundan açık listeden çıkarılmaz. (3,0) ve (4,0) güncellenir, g = rhs olduğundan tutarlıdırlar bu yüzden açık listeden çıkarılırlar. (3,1) açıldıktan sonra da hala tutarsız olduğundan açık listede kalır.

     Açık listeden minimum değere sahip eleman (3,2) seçilir. g > rhs olduğundan aşırı tutarlıdır, g = rhs = 5,2 olur. Tutarlı hale geldiği için açık listeden çıkarılır. Açılan (3,2) düğümü genişletilir. (3,1) düğümü güncellenir, yeni rhs değeri (3,2) ‘nin g değerine bağlı olarak 6,2 olur ama hala tutarlı hale gelmediği için açık listede kalır. Bu noktada robotun şuanki konumuna karşılık gelen düğüm tutarlıdır ve açık listedeki üst anahtar bu düğümün anahtar değerinden daha az değildir. Bu yüzden en uygun bulunduğu kabul edilir ve döngüden çıkılır. Yol için robotun şuanki konumundan hedef konuma doğru g değerleri takip edilir. Yani bulunulan düğüm hangi düğüm takip edilerek açıldı ise o düğüme geçiş yapılır.

     D* Lite gerçek maliyetlere odaklı çalışır. Pratikte D* Lite araması değeri g ve rhs değerlerine eklenecek olan bir sezgisel h değerine odaklanacaktır. Bu örnekte tüm düğümler için h = 0 kabul edilmiştir. Örnek D* Lite ‘nin temel versiyonudur. Son halinde şu optimizasyonlara da sahiptir;

• Her seferinde tüm komşu düğümleri düşünmeden rhs değerini güncelle
• Tüm açık listeyi yeniden sıralamadan rahat hareket ettikçe aramayı yeniden odaklama[38]

Daha detaylı bilgi için kaynaklara göz atabilirsiniz.

Kaynaklar

33. Hart, P. E., Nilsson, N. J. ve Raphael, B. “Correction to “A Formal Basis for the Heuristic Determination of Minimum Cost Paths”, SIGART Newsletter, (1972), 28-29.

34.  Hart, P.E., Nilsson N.J. ve B. Raphael, “A formal basis for the heuristic determination of minimum cost paths”, Systems Science and Cybernetics, IEEE Transactions on, 1968. 4(2): p. 100-107.

35. Yao, J., ve arkş. “Path planning for virtual human motion using improved A* star algorithm”, Information Technology: New Generations (ITNG), 2010 Seventh International Conference on. 2010. IEEE.

36. Arıcı, V., “Engellerin Bulunduğu Ortamda Gezgin Robotun En İyi Yolu Bulması ve İzlemesi”, Tez(Yüksek Lisans)– Başkent Üniversitesi, Fen Bilimleri Enstitüsü, 2008.

37. Viet, N.H., Vien, N.A., Lee, S. ve Chung, T., “Obstacle Avoidance Path Planning for Mobile Robot Based on Multi Colony Ant Algorithm Advances in Computer-Human Interaction”, Automation and Systems, (2008).

38. Ayorkor Mills-Tettey, Vincent Lee-Shue Jr. Prasad Narendra Atkar, Kevin Tantisevi, Robotic Motion Planning: A* and D* Search, Robotics Institute 16-735, http://www.cs.cmu.edu/~motionplanning/

39. Stentz, A., “The D* Algorithm for Real-Time Planning of Optimal Traverses.”, CARNEGIE-MELLON UNIV PITTSBURGH PA ROBOTICS INST, 1994.

40. https://en.wikipedia.org/wiki/D*

41. https://www.youtube.com/watch?v=e_7bSKXHvOI